Mysteries of the Mystic Rose

by Burkard Polster and Marty Ross

The Age, 22 November 2010

There’s a month to go, but Christmas decorations are already appearing. So, we decided to get into the spirit, with a very Christmassy illustration of our own.

It’s very pretty, but what is it? It may look familiar, since we used a similar diagram when discussing Prime Ministers’ birthdays. Older readers, and fans of 70’s folk art, may recall similar diagrams brought to life with coloured thread and nails hammered into wood.

The diagram is known evocatively as a mystic rose. Mathematicians, poets that they are, refer to it as the complete graph on 30 vertices. To be fair, that’s what it is: thirty points equally spaced around a circle, connected by all possible lines.

One pretty interpretation of the diagram is to imagine a gathering of 30 people, with everybody shaking hands with everybody else. Then each handshake is a represented by a connecting line: clearly a lot of handshakes. In fact, there will be 435 handshakes in total. In general, a mystic rose constructed from N points will have N x (N–1) / 2 connections.

Mystic roses with fewer points are less stunning, but they do raise an intriguing “What’s next?” puzzle. Counting the number of regions created by the first four roses, we have the sequence 0, 1, 4, 11. To find the next number we can simply draw the next rose, but the general pattern is hardly obvious.

Drawing circles around the roses appears to help, since the number of regions is now 2, 4, 8, 16. So obviously 32 comes next, right?

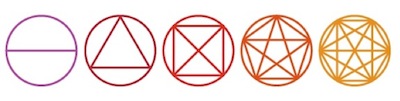
Wrong! As you can easily check, the number of regions in the orange diagram is 30, not 32. In fact this curious sequence was the topic of our very first Maths Masters effort, back in 2007.

The general formula for the number of regions is not obvious, with or without the surrounding circle. It turns out that for the mystic rose based on N points, and if N is odd, then the number of regions (without the surrounding circle) is

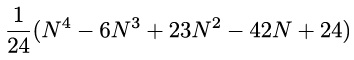
If counting the regions for odd N is tricky, counting them for even N is a nightmare. It was only in 1997 that mathematicians Bjorn Poonen and Michael Rubinstein derived a general formula. It is too gruesome to reproduce here, but the formula can be viewed in its full gory glory on our website.

Why was deriving the formula for even N so difficult? One problem with counting the regions is that we have to consider very carefully how the lines intersect. Most intersection points are created by two crossing lines, but if N is even then some intersection points are formed by three or more lines. The first such multiple intersection occurs when N = 6, at the centre of our pattern-breaker rose above.

In the process of deriving their formula, Poonen and Rubinstein stumbled across a number of curious facts. For example, it is easy to see that if N is even then N/2 lines will intersect at the centre of the rose. However, away from the centre a maximum of seven lines can intersect at a point. Furthermore, seven-line intersections only occur when N is divisible by 30. Now that is weird!

By the way, for the 30-point mystic rose there are 13800 two-line intersection points, and thousands of multiple intersection points, including 30 seven-line intersections. And for those who wish to check their counting skills, the 30-point rose has a total of 21480 regions.

One last question: why the name “Mystic Rose”? We’re not sure, but people suspect that it is because mathematical roses are reminiscent of the stained-glass windows in churches, which are known as rose windows. A perfectly Christmassy solution to our final mystery.

Puzzle to Ponder: In the 30-point mystic rose, there are clearly visible concentric circles: from where do they come?

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.