How far is 10,000 metres?

by Burkard Polster and Marty Ross

The Age, 15 February 2010

We've very much enjoyed the Winter Olympics. However, while watching the speed skating, a peculiar question came to mind: in the 10,000-metre event, how far do the skaters actually skate? One would hope it is very close to 10 kilometres. In spite of some very fussy calculations by the authorities, it would seem that this is not the case.

If the track were simply a 10 kilometer straight line there would of course be no issue. However, until the Suez Canal freezes over, we'll probably have to make do with curvy tracks, and some calculation will be required.

So, let's take a look at a typical speed skating track. It is oval in shape, made up of semicircles and straight lines. In the 10,000 metres, the track is divided into two lanes, with a skater starting in each lane.

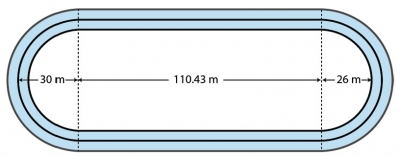
Of course the skater in the outside lane would be less than pleased to stay there the whole race. To ensure they skate the same distance, the skaters swap lanes on every lap, as indicated in the following diagram.

The track at the Olympics is designed with the intention that the red path is exactly 800 metres long, corresponding to 400 metres per lap. Note that, except in the crossover zone, the red path is 50 centimetres in from the inner edges of the lanes. This is to allow for the fact that skaters cannot skate exactly along the lane edges.

Here is the calculation for the length of one lap, taken from the official rules of the International Skating Union (ISU):

The metre distances are calculated to two decimal places, with π even given to four decimal places. It would appear that the ISU is being advised by Dennis Cometti, and is very concerned to get their distances centimetre-perfect.

However, the calculation suggests that the ISU could use a little help with their maths. Adding an extra 110.43 metres in the first line, just to subtract it again in the last line, is definitely not something a maths master would do. Also, if you calculate the total distance traveled in 25 laps, it comes to 10,000 metres plus 8 centimetres: if the ISU really cares about every last centimetre then they should use a better approximation to π, and they shouldn't round off before multiplying by 25.

Of course for us, though perhaps not for the ISU, 8 centimetres on top of 10 kilometres is nitpicking. However there is an aspect of the ISU calculation that is of genuine concern.

A top speed skater travels at around 50 km/h. At this speed, and with the sudden switches between straight segments and tight semicircles, he cannot possibly stay close to the suggested red path. He is simply bound to overshoot.

This overshooting issue is exactly why circular curves in railtracks and roads are connected to straight segments via special transition curves. However, it seems that the ISU simply doesn't care.

If you watch a skating race, you'll see that the path travelled by the skater is roughly as diagrammed below. Obviously, this is a longer curve.

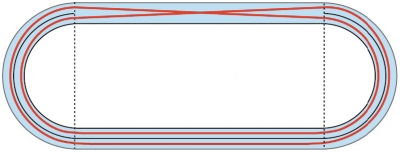
We estimate that the actual path traveled is at least 2 metres extra per lap, or an extra 50 metres in a 10,000-metre race. This is hardly ideal, unless the event is renamed the 10,050 metres. And, it makes the ISU's attempt at centimetre-perfection seem more than a trifle silly.

What's the solution? One possibility is to mimic swimming competitions, use a straight 50-metre track, and have the skaters slam into the wall at the end of each lap. Alternatively, they could simply hire some maths-savy engineers to design a track that better approximates what skaters actually do.

Puzzle to ponder

Feel free to use the comments section to suggest solutions. Later in the week we'll post our solution in the comments section.

Puzzle: Assume that a skater is always exactly 1 metre away from the inner lane edges, except along the straight paths within the crossover zone. How far would he skate in a 10,000-metre race?

Tessellation challege

The winner of our tessellation challenge in this year's first article is David Bailey from the U.K. Here is his winning entry. You can find many more of his fabulous creations on his website.

David Bailey's winning entry in the Maths Masters tessellation challenge.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.