Parabolic Playtime

Burkard Polster and Marty Ross

The Age, 27 October 2014

Your Maths Masters had some great fun recently, making parabolic jelly desserts for our little maths masters. Now we want to take a careful look at two of our favourite mathematical toys, to further demonstrate and to help demystify this parabolic magic.

Many readers will be familiar with our first toy from the impressive example at Melbourne's Scienceworks: a pair of whispering dishes. A person whispering a little in front of one of the metal dishes can be distinctly heard by their friend in front of the other dish, many metres away.

How do the dishes work? According to Scienceworks it's because "the curved shape of the dish focuses the sound". Well, um, thanks.

For those who prefer explanations to be a little more explanatory, the dishes are actually paraboloids, the 3D versions of parabolas. Associated to each paraboloid is a focal point. As we'll show later, the sound waves emanating from the focal point will bounce off the dish and travel parallel to the dish's axis of symmetry.

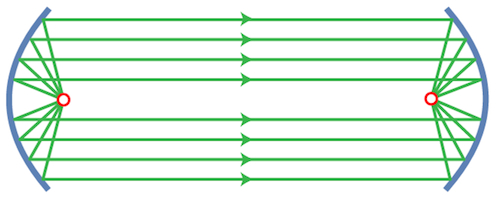
The above diagram indicates how the sound waves will be refocussed at the focal point of the second dish. However, something else needs explaining: why isn't the sound muffled? Specifically, why don't the sound waves leaving the first focal point in different directions then arrive at the second focal point at varying times?

This amounts to asking whether the green paths in the above diagram are all the same length. Indeed they are, though it's hardly obvious and the question is seldom if ever asked, much less answered. We'll also show this below but let's first play with another toy.

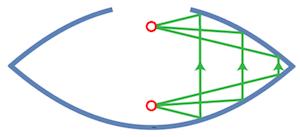
Our second toy comprises two parabolic mirrors, one containing a little hole in the middle:

Put a small object like a model car in the centre of the whole mirror, and place the second mirror on top. Then a mirage of the car will appear hovering in the hole.

It's a very impressive illusion and the underlying explanation is pretty much the same as for the whispering dishes:

It's all quite amazing and obviously little maths masters can have great fun with these toys, even without the "curvy surfaces will focus things" explanation. However your grown up Maths Masters think it's time to get busy, to really figure out how parabolas and paraboloids work. But be warned, Dear Reader: the wise masters of the Australian Curriculum have determined that focal points are unworthy of mention, so our discussion will obviously be long or difficult or boring, or all three.

Let's begin with the (hopefully) familiar y = x² parabola. Associated to this parabola are the red dot and horizontal red line pictured below.

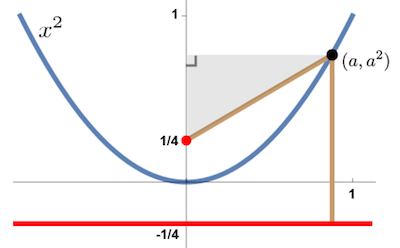
What's special about the dot and the line? A straight-forward application of Pythagoras shows that the two brown lines are the same length, which means that any point on the parabola is an equal distance from the dot and the line. This actually defines the red dot as the focal point of our parabola, and the red line as its directrix. (The ancient Greeks defined a parabola quite differently, as a special slice of a cone. They later proved that any parabola had this focus-directrix property, and our now familiar equation took another 1500 years or so to appear.)

With focal point and directrix in hand, it is now very easy to see the "equal distance" property of our whispering dishes. No matter the initial direction, the distance travelled from one focal point to the other is exactly equal to the distance between the two directrices:

Of course this simple argument assumes that the sound waves travel along the indicated paths. To justify this assumption we have to prove the fundamental property, that a ray leaving the focal point will be reflected and travel parallel to the axis of symmetry. That amounts to showing that in the diagram below the angles A and B are equal.

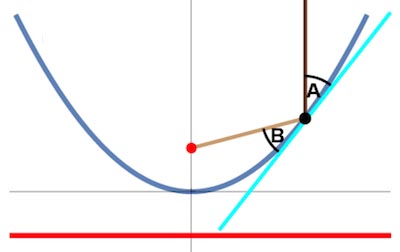
That looks like it may be difficult to prove but in fact it follows very easily from the diagram below.

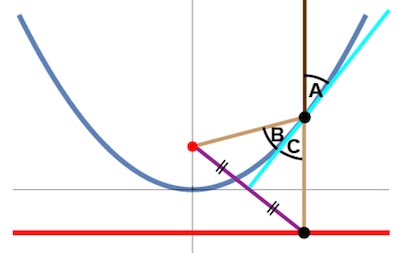
The key observation is that the blue tangent to the parabola bisects the purple segment; this can be proved with one very easy line of calculus. (The calculus can also easily be avoided, by beginning with the purple segment and showing that its perpendicular bisector hits the parabola at exactly the right point.) Now, the two triangles pictured are identical ("congruent"), and so angles B and C are equal. It is even easier to see that angles C and A are equal, and so we can conclude that A = B. We're done.

Now, was that long and difficult and boring? It's a mathematical proof, so there will be the well-rehearsed chorus of "yes" from the millions of maths-haters. But for anyone receptive to mathematical ideas the proofs are short, easy and very beautiful. And they're totally absent from the Australian Curriculum. Go figure.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.