Sneaky square dance

 

It is pleasing to know that there are parts of the world where everyone loves squares. What a paradise it must be, a country where people are forever marching in perfect square formation.

Well, maybe not. Geometric marching is probably not as much fun when its main purpose is to please a Glorious Leader.

Still, those marching squares are impressive. And, given the unfortunate folk will be marching anyway, we have a great idea for a very mathematical flourish.

Our plan is to have two identical squares of marchers, each square performing the usual stunning steps. Then, the grand finale will consist of the squares being merged into one big (Red) square.

It’d definitely be a showstopper but first there are details to sort out. The interlacing of the squares will be tricky, requiring planning, practice and fancy footwork.

We also have to decide the size of squares to use, which would need to consist of a suitable number of marchers. For example, beginning with two tiny 2 x 2 squares wouldn’t work: that would give us eight marchers in total, one short of the number required to rearrange into a 3 x 3 square. Similarly, beginning with two 3 x 3 squares of marchers would mean we have 18 marchers, too many to form a 4 x 4 square and insufficient for a 5 x 5 square.

Hmmm. This will take some time to figure out, but we should be able to do it. We’ll try 4 x 4, then 5 x 5 and so on, and eventually we should have in hand the smallest squares that work.

For now, let’s leave that calculation and just assume we’ve determined the smallest squares that can be merged. Then, imagining we have sufficient marchers to occupy those squares, we can plan the marching steps.

Let’s begin with an empty red quadrangle of just the right size to accommodate all our marchers. Then, a stylish approach would be to have the the two identical squares of marchers enter the quadrangle from opposite sides.

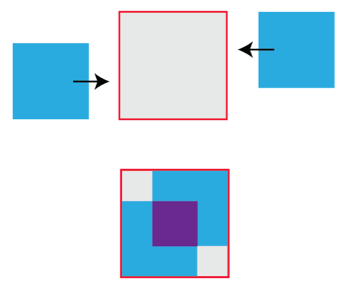
At this stage the little grey squares are unoccupied and the blue squares are overlapping. It would be crowded in the middle purple square, but that’s not a problem: we can simply arrange for half of the marchers to stand on the shoulders of the others.

Finally, we’ll have the marchers leap off their comrades’ shoulders and into the empty grey squares, a spectacular finish to our merging of the two blue squares into the Red square. Ta da!

But wait a minute. If, as planned, we have precisely the correct number of leaping marchers to fill the grey squares then this can be represented by the following picture.

Uh oh. We assumed that we began with the very smallest squares that could be merged to make a larger square. Yet, somehow we created even smaller squares that would work. How can that be?

Simply, it cannot be. Sure, there is nothing wrong with our marching plan. However, for our smallest possible squares to result in even smaller squares is a plain logical impossiblity. The unavoidable conclusion is that no squares can be merged in the way we had originally contemplated.

Well, bum. So much for our plans to impress the Glorious Leader with a great marching finale. However, perhaps he’ll be impressed by some intriguing mathematics that emerges from our failed attempt.

What we have outlined above is a proof by contradiction. We began by assuming that certain squares were possible, and that assumption led to a contradiction, a logical impossibility. This contradiction proves that our original assumption was wrong, and that no such squares can exist.

We can now reconsider this conclusion in terms of numbers rather than squares. Consider again the two hypothetical blue squares. Say each square contains B x B marchers and that the larger red square into which they can supposedly merge has R x R marchers. We have proved this is impossible, and that means that there are no positive whole numbers B and R that solve the equation

2B² = R²

Rearranging, it follows that there is no fraction R/B that solves the equation

 (R/B)² = 2

So, there is no fraction whose square is 2, which is exactly the same as saying √2 is not a fraction. That is, our marching ponderings have proved that √2 is irrational!

Now that is pretty cool. It is one thing to punch √2 into a calculator and to stare at a few unilluminating decimals; it is another to know that √2 can never be written as a fraction.

We’ve written about √2 before, when discussing the clever principle behind the dimensions of A-sized paper. On another occasion we used base arithmetic to give a different proof that √2 is irrational.

There are a number of proofs that √2 is irrational, but the marching band proof above is probably our favourite. It has been popularised by the great John Conway, who attributed it to mathematician Stanley Tennenbaum.

And will the Glorious Leader be impressed with Tennenbaum’s proof? We don’t know. But if he isn’t, we think it’s probably time to start looking for a new Glorious Leader.

 

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators (and iPads) with a hammer.

Copyright 2004-∞ All rights reserved.