Uncovering Base Motives

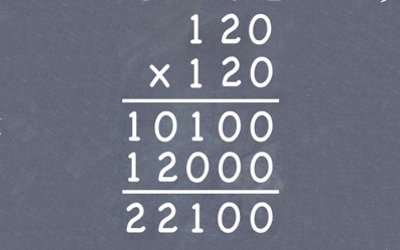
Once upon a time, many years ago, there was a review of the school mathematics curriculum. In those days it was believed that mathematicians could contribute some insight. The good mathematicians were pleased to assist, and the result was a brilliant curriculum. The teachers and students were delighted, and everybody learned mathematics happily ever after.

Well, not quite. Our tale is of the "New Maths" movement, from the 1960s. The New Maths did include a significant involvement of mathematicians, and the proposals were indeed mathematically sophisticated, but overall the results were farcical. It is perhaps the reason why mathematicians to this day reside in pedagogical purgatory.

A brilliant encapsulation of what went wrong is provided by Tom Lehrer's famous and funny song, New Math. Lehrer invites his audience to subtract 173 from 342. Having barely coped with that, Lehrer then declares that the subtraction should actually be done in base eight, chirpily singing that the 4 is in the "eights place", the 1 is in the "sixty-fours place", and so on. Lehrer's lesson is hilarious, full of New Maths jargon, and all of it self-evidently pointless.

Arithmetic in anything but base ten has now disappeared entirely from the curriculum, and we bid good riddance to the nonsense lampooned by Lehrer. But why were these bases ever taught at all? Have we lost anything by their removal? Indeed, we have: the bases have been thrown out with the bathwater.

One purpose of using different bases is simply to have fun, to play with numbers. True, writing π in other bases may not appeal to everyone. However, we at least enjoyed the exercise when trying to determine our ideal number plate. But there is also a deeper message here.

Numbers are abstract. They are ideal, mental objects, difficult to discern and difficult to discuss. Because of this it is very easy, for example, to confuse the numeral "8", the symbol, with the number that the symbol stands for. Sadly, many current textbooks are riddled with such confusion.

Writing a number in different bases can be an attempt to distinguish the number from the symbols representing that number. Admittedly, the attempt may be so abstruse that the message is lost, and then we sing along with Tom Lehrer. However, given the current infestation of calculators, it is now common to view decimal representations as the be all and end all, to regard these decimals themselves as the numbers. They are not numbers, and they are usually not even insightful representations of numbers: this message is more important than ever.

That's all very general, so what about particular bases? The ancient inventor of our number system chose base ten simply because humans have ten fingers. However, in certain contexts there are other natural bases. The clear example is base two, where all numbers are built up from 0 and 1. The on-or-off nature of base two arithmetic makes it perfect for the logic underlying computers, and for many related areas of mathematics. Indeed, given the technology fetishism of our curriculum masters, the absence of base two in the national curriculum is particularly puzzling.

Other bases have uses as well, and we'll end with a truly beautiful illustration. We recently wrote about irrational numbers. We remarked that when numbers such as √2 are declared irrational it is usually with no hint of how we know them to be irrational. Well, now we will ponder that.

Recall that √2 being irrational means that it could not be written as a fraction, √2 = A/B with A and B whole numbers. If we square both sides of this equation, and multiply to get rid of the denominator, we then have the equation

A² = 2B².

So, what we are claiming is that this equation is impossible, that no positive whole numbers A and B will solve it. But how can we possibly rule out all of the infinitely many choices for A and B? Here comes the magic: we shall imagine that the numbers A and B are written in base three.

A number written in base three will have a ones place, a threes place, a nines place and so on. So, for example, we would normally write the number fifteen as 15, but in base three it would be written as 120: this amounts to (0 x 1) + (2 x 3) + (1 x 9).

We can perform arithmetic in base three just as in base ten. For example, in our graphic at the top of the page we have multiplied 120 by itself: if you wish to work through the details, we have provided them here. However, for what follows you only need to know one fact about base three arithmetic: ignoring the final zeroes, any squared number always ends in a 1.

Now, look again at our equation for √2. Written in base three, we now know that the A² will end in a 1. However, B² will also end in a 1, and so 2B² will end in a 2. It follows that the sides can't match, that the equation is impossible to solve, and so √2 cannot be written as a fraction. We have proved that √2 is irrational!

Tom Lehrer is himself a mathematician, and we imagine that even the sceptical Lehrer would be captivated by this beautiful application of base arithmetic.

Puzzle to Ponder: Feel free to suggest solutions in the comments section. Please also email us if you wish to be added to our email list.

Why does any squared number end in a 1 when written in base three? Can other bases be used to prove that √2 is irrational? Are there other square root or cube root numbers that can similarly shown to be irrational?

Free Public Lecture, Sunday August 1: Marty will give a talk entitled Mathematics education: Australia's very own Titanic. Melbourne Museum, 11:30-12:30. For more information, please visit the MAV website.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.