Winning formula but is it cricket?

By Burkard Polster and Marty Ross

The Age, 4 February 2008

If a game is interrupted, how do we decide the winner? We could simply declare the game a draw, but if one player is well in front they could justifiably feel this is unfair. And in professional games there are often other incentives for declaring a winner.

In our modern world, the notorious scenario for this question is one-day cricket, and what to do when rain interferes. Equally notorious is Duckworth-Lewis, the currently sanctioned method for adjusting the game. We’ll try to make D-L less notorious by giving a simple explanation of how it works.

Let’s imagine Australia (yay!) and India (boo!) are playing a match, Australia bats first and scores 300 runs in their 50 overs. Then the rains come down, and the match is shortened to 30 overs each. How many runs should India have to score to win?

The simplest approach is to take Australia’s average rate of 6 runs per over, and then multiply that by 30. So, India would have to score 180 runs to tie, with one more to win. But this would obviously be unfair to Australia. With only 30 overs, India’s batsmen could afford to be more reckless, making their task easier. So, India should have to score more than 180 runs, but how many more?

There is no definitive answer. We just have to look at the statistical evidence of how teams score their runs. Then, any method of adjustment will be a compromise between accuracy and simplicity. Duckworth-Lewis, first used in 1997, is such a compromise.

The D-L approach is to consider the “resources” of each team, consisting of their 10 wickets and their 50 overs. In the example above Australia used all their resources, but India had some of theirs taken away. To estimate how much, Duckworth and Lewis modeled how teams score (they used exponential functions) and created a table like the one below.

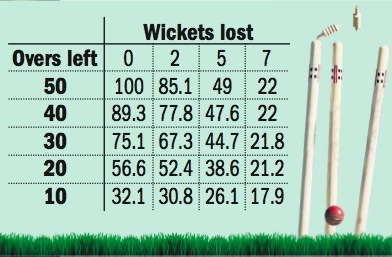
Initially a team has 100% of their resources, but this declines as the overs are used and the wickets fall. For example, with 40 overs left and 7 wickets lost, the table indicates that only 22% of the team’s resources are left.

With this approach we have an easy method of analyzing games like the above. India has 10 wickets and 30 overs, which amounts to 75.1%, about 3/4, of their resources. Since Australia had 100% of their resources, India should only have to make 3/4 of Australia’s runs. Then, 3/4 of 300 is 225 and so that is their target, with 226 to win.

D-L is not perfect, but it is relatively simple and very flexible. For example, suppose in the next game Australia again bats first and again scores 300 runs. Then India scores 200 runs in their first 30 overs, without losing any wickets, and then the rains come down. Who should be declared the winner? You have to decide what percentage of India’s resources they have lost: email us for the exciting conclusion!

But is D-L fair? The evidence is that it works very well. In 2004 Duckworth and Lewis looked at the effect of their system, analyzing over 1000 games. They calculated that in completed games, the team batting first won about 52% of the time. And, in games where D-L was applied, the team batting first won about 53% of the time. This is very good agreement!

Still, Duckworth and Lewis were unhappy. They had evidence that their system did not work as well when one team made a huge score, so they adjusted their method. Now, tables are no longer sufficient, and the calculation is done by computers. And, D-L now works even better. But is it cricket?