Ringing the changes

By Burkard Polster and Marty Ross

The Age, 15 October 2007

Do you like your maths in exotic locations? Then why not join the band of bell ringers at St. Paul’s Cathedral for the ringing of the changes. What does bell ringing have to do with maths? A lot! We’ll explain.

St Paul’s – the church opposite Federation Square - has twelve main bells, tuned in the key of C# major. The smallest bell, no. 1, rings the highest note, with the largest bell, no. 12, ringing the lowest. Changes can be rung using any number of bells. So, let’s simplify things, and just use bells 1, 2, 3, and 4.

A change is what mathematicians call a permutation, the ringing of each of the four bells exactly once. For example, 3214 refers to the change of ringing bell 3, then bell 2, and so on. Then, ringing the changes means to ring a sequence of changes, whilst obeying three mathematical rules: first, the sequence starts and ends with the change 1234; second, except for the start and end, no change is repeated; third, from one change to the next, any bell can move by at most one position in its order of ringing. For example, the third rule says that the change 3214 cannot be followed by 2134.

One possible sequence of changes, known as Plain Bob, goes like this:

Here we first move down the first column, then the second and finally the third. Have a close look and you can see the third rule in action---from one change to the next a bell will either stay in the same position or swap its place with a neighbouring bell. In the diagram, these swaps are indicated by crosses between the two changes.

Here are a few facts to set things into perspective. To ring one change takes between 1.5 to 2.5 seconds, the time it takes a bell to complete a natural swing. When bell ringers “go wild”, they will ring sequences of changes consisting of more than 5000 changes, which translates into several hours of “amusement” for the neighbours. When ringing the changes, bell ringers are not allowed any memory aids such as sheet music, nor can they be relieved by another bell ringer (for example, to “relieve” themselves). So, this means that a bell ringer has to effectively recite a sequence of several thousand numbers, one every two seconds, and to translate this sequence into perfect bell ringing. It takes a bell ringer several months to master ringing a bell by themself, and years before they can dream of performing this kind of marathon bell ringing as a member of a team.

When ringing bells, one of the grand aims is to ring a sequence that includes every possible change. In the case of four bells such a sequence must be 1 x 2 x 3 x 4 + 1 = 25 changes long, and Plain Bob is such an example. The general formula for n bells tells us that 1 x 2 x 3 x...x n + 1 changes are required.

Mathematicians have only recently proved that, no matter how many bells we want to ring, it is always possible to compose a complete ringing sequence. Here is a table that shows you what numbers of changes we are talking about, and how long it would take if you rang at a rate of two seconds per change.

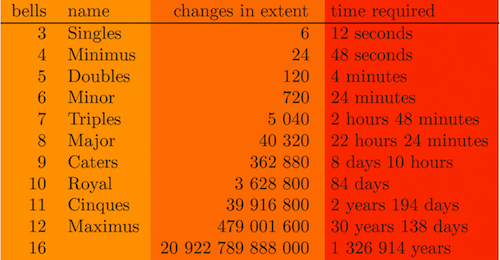
To ring a complete sequence on eight bells is the most that seems humanly possible. In recorded history, such a sequence has been rung on church tower bells only once. This took place at the Loughborough Bell Foundry in the U.K., beginning at 6.52 a.m. on 27 July 1963 and ending at 12.50 a.m. 28th July after 17 hours 58 minutes of continuous ringing (did they really not go to the toilet for 18 hours?). Of course, to actually do this is ridiculously hard, both physically and mentally. So how do they do it? One mental trick is to make up sequences that are as easy to remember as possible. If you have a close look at Plain Bob, you can see that each column is generated from the change at the top by a simple “knitting pattern of swaps”. Then, at the end of the first and second columns, you swap the last two bells and in this way link the three columns together. Based on this simple algorithm, it is very easy to reconstruct the whole sequence from scratch. Try it!

Permutations and collections of permutations play very important roles in many branches of mathematics. In particular, group theory, that branch of mathematics concerned with symmetries, is full of permutations. The earliest examples of group theory structures and techniques in action are the highly structured bell-ringing sequences that were developed in the early 17th century. For example, the first column of our sample sequence captures the eight symmetries of the square and the subdivision of the ringing sequence into three columns is something that mathematicians also get excited about.

But why on Earth did anybody dream up this convoluted mathematical way of ringing the bells, instead of just playing tunes? And, how did they get away with doing so for centuries? After all, lots of people do complain about the noise, and together with the bell tower itself the bells do form a musical instrument that you could in theory play tunes on by striking the bells with hammers. The problem is that if you want to ring the bells by swinging them, which sounds a lot more impressive, and carries a lot further, ringing tunes is not an option. Why? The reason is that we are talking about very large bells (up to 1.5 tons in the case of St Paul’s). Once set in motion it is very hard for a bell ringer to vary the interval at which such a monster bell will ring. This is the mechanical constraint that explains the third rule of bell ringing, and motivated bell ringers to invent mathematically perfect bell ringing.

Originally, change ringing was a competitive sport, with bands of ringers of footy player physique and mindset, competing against each other on a regular basis. Often at odds with the church itself, the exercise, as it is traditionally called, had as much do with ringing bells as with shouting each other drinks according to very intricate penalty system for mess-ups. Bell ringing has come a long way and mellowed a bit since its bloodsport origins (see www.anzab.org.au for more information). However, if you are interested in maths, beer, and serious mind games, do visit one of six bell towers in Melbourne where bell ringing is still practised.