A square full of triangles

By Burkard Polster and Marty Ross

The Age, 30 July 2007

Federation Square–you hate it, you love it, … or you simply got used to it. Impolitely, one could describe it as an amorphous assortment of buildings covered with bathroom tiling. But the bathroom tiles are very different from your ordinary boring squares and hexagons. You may have heard of it referred to as the pinwheel tiling, but were perhaps too scared to ask what this means. Well, here is the simple rule which explains it all.

We begin with a so-called golden triangle. This is a right-angled triangle in which the middle-length side is twice the length of the shortest side.

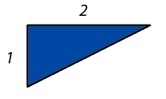
Draw four more triangles to make a larger super-triangle, like this:

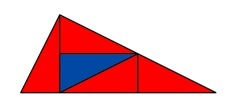
Next, in exactly the same way, draw four more copies of the super-triangle to build a super-super-triangle. Now keep going, either until you get bored or, if you are a Federation Square architect, until you have covered the whole wall.

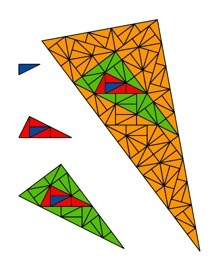
Very simple, isn’t it? Looking closer at the diagram, notice that the different-size triangles are pointing in different directions. In fact, if you think of successive stages of this process as frames of a movie, then what you see when you watch this movie is a triangle that grows from frame to frame and turns in the clockwise direction, something very reminiscent of the blades of a pinwheel toy rotating in the wind. Hence the name “pinwheel tiling”.

The pinwheel tiling is one of the many ingenious discoveries of the great Princeton mathematician John Conway. Mathematicians (and architects) love such tilings - the RMIT façade on Swanston Street gives another example - because of the intriguing manner in which the tilings grow. Though the rules are simple, these tilings never repeat in the same way as your off-the-shelf bathroom tilings. In fact, in a strict mathematical sense they don’t repeat at all. So, whatever else one might say, at least Federation Square is not predictable.