Christmas comes but once, or does it ...

by Burkard Polster and Marty Ross

The Age, 15 November 2007

People are starting to get serious about Christmas: felling innocent pine trees, stocking up on supplies for the holidays and, of course, compiling wish lists of presents to guide compliant loved ones. When you compile your wish list, it is profitable to stick with the following well-known formula:

On the first Day of Christmas my true love should give to me one X (for eXpensive). On the second Day of Christmas my true love should give to two Y and one X. On the third Day of Christmas my true love should give to me three Z, two Y and one X.

And so forth. Traditionally you should begin twelve days before Christmas. However, shops nowadays have already truly begun their Christmas campaigns by September. So, you can probably extend a modern list to a hundred days.

The presents you receive on a given day combine to form a pretty triangular Christmas tree, as shown in the diagram for day six of the traditional lineup of gifts.

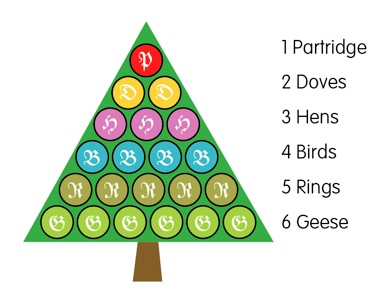
The number of presents that you receive on the N’th Day of Christmas is equal to the sum 1+2+3+4+…+N. So, on consecutive days you receive 1, 3, 6, 10, 15, … presents. What about Day 100? To calculate this sum appears to be very unholiday-like work, but there is a magical, mathematical shortcut, worthy of Christmas.

According to a popular story Carl Friedrich Gauss (1777-1855), one of the greatest mathematicians ever, discovered this trick for himself when he was only seven years old. Gauss’s teacher had asked the class to add up all the numbers to 100, and the answer apparently came to Gauss in a flash. Nobody really knows how he did this, but it was probably very much like the following.

Rearrange your triangular tree of presents for Day N into a right-angled triangle, as shown in the diagram. Notice that two copies of this new triangle fit together into a rectangle with N rows, each of N+1 presents.

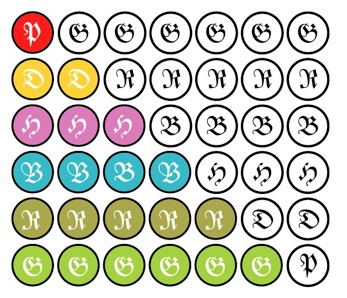
This means that the sum that you are after is 1/2 the number of circles in this rectangle, namely N(N+1)/2. Just like Gauss, you can conclude in a flash that on the 100’th Day of Christmas you receive 100 x 101/2 = 5050 presents. Simple!

Of course, we are not yet finished. After all, we are not only receiving presents on one of the Days of Christmas, but on every day. So, on the N’th Day of Christmas we’ll be the proud owners of all the presents we received on day one, plus those that we received on day two, and so on. That is, we receive a total of 1+3+6+10+…+ N(N+1)/2 presents. Using another ingenious trick, mathematicians have shown that the formula for this sum is N(N+1)(N+2)/6. (Email us, and we’ll send you this trick as our Christmas present.)

So what is the maximum number of presents you can score this way? Just begin on Boxing Day, and make every day a Day of Christmas! Then, by the 365th day of Christmas, you will have accumulated 365 x 366 x 367/6 = 8,171,255 presents. If you are less greedy, you can stick with the traditional twelve days format and use our formulas to calculate your haul. Though not as impressively huge a swag, you’ll find your year conveniently gift-filled. Merry Christmas!