Six degrees of mathematician

Are you distantly related to a really famous person? How could you find out? Well, if you’re a mathematician then the Mathematics Genealogy Project can definitely help.

This database has recorded the PhD supervisors of more than 150,000 past and present mathematicians. Beginning with any mathematician, one can instantaneously find out their supervisor, their supervisor’s supervisor and so on, back for centuries.

Trying this on ourselves (and sticking with the principal supervisors), the database produced the following histories:

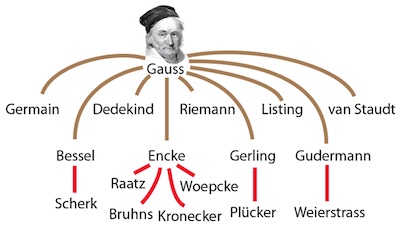
Burkard Polster < Strambach < Salzmann < Pickert < Hasse < Hensel < Kronecker < Encke < Gauss < Pfaff < Kastner < Hausen < Wichmansshausen < Mencke < Thomasius < Leibniz

Marty Ross < White < Almgren < Federer < Morse < Adams < Birkhoff < Moore < Newton (not THE Newton) < Chasles < Poisson < Lagrange < Euler < Bernoulli Jo. < Bernoulli Ja. < Werenfels < Zwinger

It’s definitely time to celebrate, since both Maths Masters are direct descendants of mathematical royalty: Gauss and Leibniz in the case of Burkard; Euler and the Bernoullis in the case of Marty. 

What does it mean? For one thing, it means that the ghosts of some great mathematicians will be less than thrilled with a couple of their descendants.

Let’s take a closer look. It turns out that the great Carl Friedrich Gauss has a total of 54,539 descendants. That is, more than a third of all mathematicians in the database are descendants of Gauss. Since Gottfried Leibniz is earlier in Burkard’s ancestry, Leibniz must have even more descendants than Gauss. In fact, Leibniz has 87,443 descendants, more than half the mathematicians in the database, and it’s pretty much the same for Leonhard Euler. So, being the descendant of a great mathematician is very much not a big deal.

Taking a step sideways, it turns out that the vast majority of mathematicians are cousins: if one includes co-supervisors, about 85% mathematicians are in one huge student-supervisor extended family. 

Apart from a bit of fun, which is mostly what genealogy seems to be about, the database has at least one serious application. Some mathematical journals and grant bodies now use the database to attempt to avoid conflicts of interest, such as a supervisor assessing a grant application or research article of a student.

There is another type of kinship, which mathematicians have been having fun with for years: connections via co-authored papers. MathSciNet is a huge database, which records all types of information about mathematical research articles. The database lists about 500,000 authors, and the co-authorship of articles establishes a huge network.

This offers another method of snuggling up to mathematical fame: pick a famous mathematician, say K. F. Gauss, and then calculate how many co-authors are required to connect to them. So, your distance from Gauss is 1 if you and Gauss have collaborated on an article. Given that Gauss died more than 150 years ago, that’s a little unlikely. Still, you could have distance 2 from Gauss if you collaborated with a collaborator of Gauss’s, and so on. In fact, both Burkard and Marty are distance 7 from Gauss.

It’s difficult to connect to mathematicians from Gauss’s time or earlier, because co-authorship was then uncommon. However, these days more than half of all mathematics articles are co-authored, and the distances tend to be extraordinarily short. There is also a webpage that will calculate the distances between authors. 

The most popular starting point for this distance game is the brilliant, wildly eccentric and incredibly prolific Paul Erdős. In his lifetime, Erdős wrote about 1500 articles, almost all of them co-authored with other mathematicians. 

The distance of a person from Erdős is referred to as their Erdős number. Both Maths Masters have an Erdős number of 4, which sounds pretty impressive. Except, the average Erdős number is about 5. 

Going one step further, an engaging 2004 study of the collaboration network determined that mathematicians with an Erdős number were on average about a distance 8 apart. So, pretty much eight degrees of separation of almost all mathematicians. It definitely is a small mathematical world.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator. 

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.