A Victa-ry for mathematics

by Burkard Polster and Marty Ross

The Age, 14 January 2011

The grass is long, and guess whose job it is to cut it? Confronted with this tedious chore, a Maths Master has only one possible course of action: he must immediately retire to his office, to determine the mathematically best way to mow the lawn.

Clearly what is optimal for a lazy Maths Master is to push the lawnmower the shortest distance possible. So, he wants to avoid mowing twice over the same patch of lawn. Let’s see what he might have to consider.

As we push the mower, its circular slashing disc cuts a swath through the grass. If we travel in a straight path, then the cleared region will be a corresponding thick line.

Think of the straight path as consisting of four shorter segments. Now, rotate somehow at the three joins to create a new, crooked path.

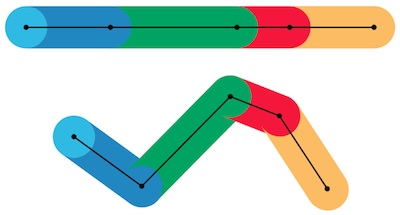
Of course the straight and crooked paths are of exactly the same length. However, the crookedness creates some extra overlap at each junction, and so the area of the surrounding mown region will be lower. And, the sharper the angles, the greater this wasted overlap.

It is therefore beneficial to try to mow along paths that are as straight as possible. However, before someone declares the problem solved, and especially before they hustle us out to do some mowing, we need to think about how to determine such “straight paths” for a whole lawn.

It is also worth mentioning that such analysis has other applications, just as important as improving mowing technique. For example, consider a helicopter searching for a person lost at sea. The helicopter should survey as much ocean as quickly as possible. And, at any moment, the search team can survey a circular patch of ocean surrounding the helicopter. So, this search problem is mathematically similar to our problem of mowing as efficiently as possible.

Of course, the practical concerns of the two problems are very different. When searching for someone lost at sea, time is of the essence, and any overlap is a serious issue. As well, searching over a large, uninterrupted body of water, we can quickly decide upon a suitable search: for example, begin where the person was last sighted, and then search in an expanding spiral path.

On the other hand, suppose we have our lawn in front of us and we want to determine a good path. In practice most lawns are small and quite regular in shape. So, a little trial and error usually suffices to come up with a suitably efficient mowing path. However, if we need to mow a golf course the problem is trickier.

For most large (and more realistic) optimising problems, the trick is to make them manageable by simplifying them, and by being satisfied with a close-to-best solution. Then, practical solutions will come from a computer.

For example, we can simplify our golf course mowing problem by covering the course with an array of circles, as pictured, with each circle radius equal to the width of the mower disc.

Connecting the centres of the circles produces an equilateral triangular grid, with vertices at the circle centres. Following a path consisting of grid edges, there will necessarily be a fair amount of overlap.

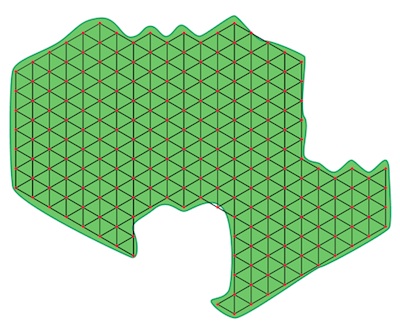
The advantage is, as long as all vertices are included in the path, we can be sure that the whole lawn will be mowed. As well, the efficiency of a path no longer depends upon straightness, and is measured simply by the number of edges travelled: the best we can hope for is to travel along one fewer edge than the number of vertices.

So, a path will be relatively efficient if few or no vertices are visited more than once. Finding such an efficient path is easily achieved by well-known computer search algorithms.

So, we now have an elegantly mathematical approach to mowing the lawn. But, alas, that analysis took a while, and it seems to be getting dark. The mowing will just have to wait until next weekend.

Puzzle to ponder: Suppose you have a lawn that is 200 square meters in area and your mower disc is 70 cm in diameter. Show that any mowing path for this lawn must be at least 280 metres in length.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.