Cycling in circles

by Burkard Polster and Marty Ross

The Age, 19 July 2010

As the Tour de France continues, it has been great fun to watch riders on those long, mountainous routes. However, we have discovered that it might be even more fun if they simply rode in circles.

Take some chalk and draw on the ground a big loop without indentations (what mathematicians call a closed convex curve). Now ride your bicycle so that the back wheel follows the path of the loop. As you do so, the front wheel traces another, larger loop. Together, the two loops bound the grey ring pictured. Then, regardless of the shape and size of the loops, the area of the ring will always be the same.

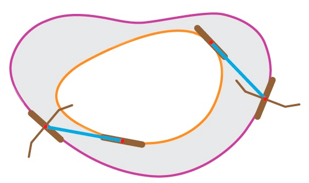
In fact, if your bike is length L from wheel hub to wheel hub, then the area of the ring is always πL². That's very cool, though the familiar formula suggests something of what's going on.

Imagine the original "loop" is simply a point, and so the back wheel remains stationary. Then the loop traced out by the front wheel is exactly a circle of radius L, and our formula simply gives the area of this circle.

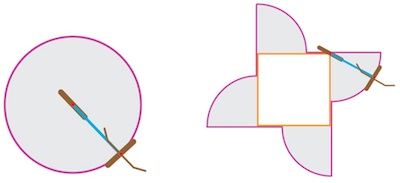
What if we start with a real loop? As a second example, imagine that the inner loop is a square. Then it is not hard to see that the outer loop traces out four extra quarter circles, and the area formula then follows again.

In fact, exactly the same argument works when the inner loop is any convex polygon. Finally, for a genuine, curvy loop, the formula follows by approximating the loop by polygons. Easy!

You can also check that in both of the examples above the length of the outer loop is 2πL larger than the length of the inner loop, and this formula is also true for convex polygons. So, maybe that's another formula that is always true? No! The length formula definitely fails whenever the inner loop is genuinely curvy. We'll leave it for you to ponder why approximating by polygons doesn't work here.

All of this is reminiscent of our column on wheelchair racing champion Kurt Fearnley, in which we had Kurt ride around in loops. If Kurt's wheelchair is of width L then we found that the length of the outer loop will indeed always be 2πL longer than the inner loop, but the area formula is not true in this scenario.

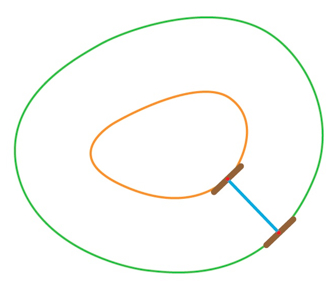
Also, with bicycle maths in hand, you may wish to revisit a problem from last year's Age Math Challenge.

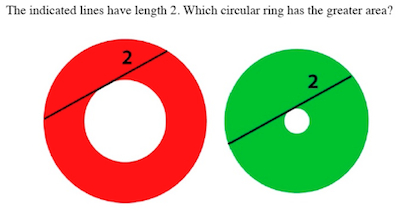
Can you now see at a glance why the two rings have the same area?

Puzzle to Ponder: Here is a 3D version of the above bicycle maths. You make a bead for a necklace by drilling a cylindrical hole through the centre of a solid plastic ball. If the resulting bead is 1 centimetre high (when resting on the hole created), what is the volume of the bead?

Feel free to suggest solutions in the comments section. Please also email us if you wish to be added to our email list.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.