Which way did Natalie go?

by Burkard Polster and Marty Ross

The Age, 12 July 2010

The Tour de France is well under way and, much to our surprise, this year's route seems to have taken in the Clayton campus of Monash University.

The evidence is in the above photo, showing tyre tracks in the wet cement.

The junior Maths Masters in the foreground are trying to get to the bottom of this. With brilliant detective work, they have already deduced that the stray cyclist is someone named Natalie. They made this deduction from viewing Natalie's signing of her masterpiece in the lower left corner.

The detectives now want to figure out which track was made by the front wheel and which by the back wheel. And, they want to determine in which direction Natalie was riding.

Sherlock Holmes and his sidekick Watson puzzled over the same problem in The Adventure of the Priory School:

"This track, as you perceive, was made by a rider who was going from the direction of the school." "Or towards it?" "No, no, my dear Watson. The more deeply sunk impression is, of course, the hind wheel, upon which the weight rests. You perceive several places where it has passed across and obliterated the more shallow mark of the front one. It was undoubtedly heading away from the school."

Holmes is unquestionably a great detective, but in this instance he is, well, off track. Regardless of the direction of travel, if there is a crossing then it is the back track crossing over the front track. So, all that you are able to deduce is which track was made by which wheel, and not, as suggested, the direction of travel.

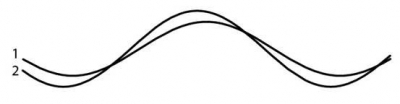
Can we do better than Sherlock Holmes? The following is an aerial view of a bicycle leaving a pair of tracks as it travels from left to right.

Notice that the back wheel is always pointing towards the middle of the front wheel, and remains a fixed distance behind. A second crucial observation is that the back wheel is always tangent to its track: the back wheel is pointing in the line of its motion. Finally, the back track is generally less curvy than the front track.

Using these observations it is usually very easy to solve bicycle track puzzles, even without Holmes's insight into the back track crossing on top of the front track. For example, in the following picture track 1 is clearly less wavy, which suggests that it is the back track.

Next, we can draw some tangents to this back track and see where they intersect the front track.

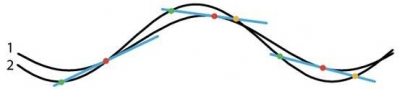
If the bicycle were travelling to the right, the orange point would mark the corresponding position of the front wheel; if travelling to the left, the green point indicates the front wheel. But the distance between the orange point and red point keeps changing, which is impossible. By contrast, the distance between the green point and the red point is always the same. So, we can conclude that the green point correctly indicates the front wheel, and therefore the bicycle was travelling to the left.

This doesn't always work. If you ride your bicycle in a circle then the two tracks will be concentric circles, and the circles will be the same no matter the direction you ride. Or, if you ride in a perfectly straight line then you'll see only one track. And, incredibly, there are other bicycle tracks that can be traversed in either direction, and other "unicycle tracks" where the back wheel exactly follows the front. But these weird tracks are pretty much impossible to ride: in practice, our detective procedure works very well.

Now, back to Natalie's tracks. Below we have reproduced a bird's eye view of her tracks, and you should have no trouble determining Natalie's direction. Or, if you happen to spot Natalie at the finish of the Tour, then do please ask her for us.

Feel free to suggest solutions in the comments section. Please also email us if you wish to be added to our email list.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.