The ball was in AND out? You cannot be serious!

by Burkard Polster and Marty Ross

The Age, 21 June 2010

Wimbledon begins tonight, and your Maths Masters are nostalgic for John McEnroe. We remember McEnroe's epic battles with Björn Borg, and also his terrific tantrums. But just imagine McEnroe's reaction if he had been told that Borg's serve was definitely out, but that no linesman was permitted to call it. Can we be serious?

The following diagram shows the skidmarks of some of Borg's serves from the far side into the near right-hand court. The brown marks indicate serves that were in and the orange marks indicate faults. We've also identified the sharp-eyed linesmen keeping watch on the three lines bounding the service box.

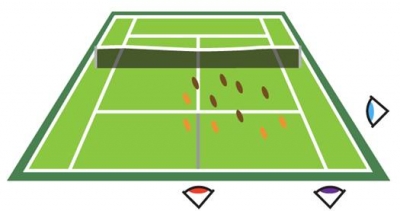
Each linesman checks the ball only in relation to his line. He yells "FAULT!" if the ball is completely on the wrong side of his line, and remains silent otherwise. If all three linesmen are silent then the ball is taken to be in.

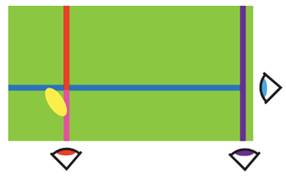
Now consider the diagram below, showing the yellow skidmark of one of Borg's faults. The purple linesmen will definitely keep silent since the ball is far to the correct side of his line. But both the red and blue linesmen will view part of the ball as level with their line, and so they will keep silent as well. So, though the ball is definitely a fault, no linesman is permitted to call it! At which point, McEnroe presumably hurls his racquet.

Of course, balls are much more commonly miscalled simply as a result of human error. Which is why the infallible computer system known as Hawk-Eye was introduced. How do we know Hawk-Eye is infallible? Because the tennis commentators constantly act as if Hawk-Eye is infallible. Hmm.

Hawk-Eye will occasionally get it wrong, of course, notwithstanding some confusing hype on the official website. Hawk-Eye takes video footage from up to ten high-speed cameras and uses the footage to reconstruct the trajectory of the ball. But any such filming and reconstruction will always contain some approximation and some error.

The International Tennis Federation demands that any electronic system must never be in error by more than 10 millimetres, and that the average error must be below 5 millimetres. It is claimed that Hawk-eye is accurate well within these tolerances. However, as British academics Harry Collins and Robert Evans have noted, precise details of the testing of Hawk-Eye are not made available. This makes it difficult to know exactly what is true, or even what "average error" means in the context of these tests.

We have little doubt that, though not perfect, Hawk-Eye is in general very accurate. However, we do not believe that Hawk-Eye will always be accurate to within 10 millimetres. With just the wrong ball trajectory, Hawk-Eye could definitely be out by centimetres.

Imagine a ball shooting across the ground at a very shallow trajectory. Here, even tiny errors in Hawk-Eye's calculations can create huge errors in determining the precise location of where the ball actually touches the ground. And of course Wimbledon's grass court, with its natural unevenness, does not make things any easier.

You might argue that the high tennis net rules out such skimming shots. However, since balls can also be hit around the net, not just over it, these troublesome trajectories can definitely occur. In such situations, it is not clear that Hawk-Eye will be more accurate than the linesmen.

Obviously such occurrences are rare, and Hawk-Eye is in general of great assistance to quality linecalling. But we do get annoyed when gullible commentators treat video simulations as if they were reality. We wish we had McEnroe by our side to say it for us: they cannot be serious!

Puzzle to Ponder: Feel free to suggest solutions in the comments section. Please also email us if you wish to be added to our email list.

How might you adjust the use of the linesmen to avoid the paradoxical linecall we considered above?

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.