How round is your soccer ball?

 
It's time for the World Cup! So we're going to need plenty of good, round soccer balls. And how to make a perfectly round sphere? Blow a soap bubble!

Unfortunately, Harry Kewell has steadfastly refused to use soap bubbles for his penalty kicks. An alternative is to work with the Famous Five regular solids. First, sew together some flat leather polygons to form the solids. Then, inflating the polyhedrons, the sides of the solids will bulge into a roughly spherical form.

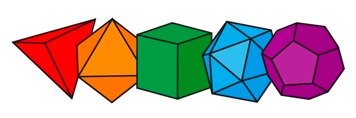
Predictably, this works poorly for the cube and the two pointier solids. However, the blue icosahedron and the purple dodecahedron work reasonably well. In fact, we own a commercially made dodecahedral ball.

A standard soccer ball is a variation of this idea. It consists of 12 pentagonal and 20 hexagonal panels. It can be thought of as an icosahedron with its 12 corners sliced off, and with patches sewn over the resulting pentagonal holes.

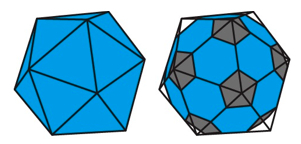
There is still a decision to be made: how large should you make the pentagonal holes and patches? A natural mathematical approach is to ensure all the edges of all the panels have the same length. However, this makes the hexagons much wider than the pentagons, which in turn results in markedly different bulging of the two types of panels.

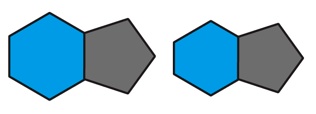
To even out the bulging, better quality balls are constructed using slightly larger pentagons. That requires the sides of the hexagons to have two slightly different lengths, and so the hexagons are no longer perfectly symmetric.

After all that, you finally have your soccer ball. Will FIFA, the governing body for soccer, judge your ball sufficiently round for a good game of soccer? They actually have a very nice website that explains the tests they perform.

A soccer ball consists of 20 + 12 = 32 panels, each panel facing a similar panel on the opposite side of the ball. That gives 16 pairs of panels, and for each pair FIFA measures the distance between the centre points of the opposing panels.

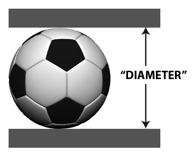
This procedure gives 16 "diameters" of the soccer ball, and ideally all these diameters would be equal. In practice, FIFA calculates the average of the 16 diameters, and then declares the ball to be "round" if no individual diameter differs from the average by more than 2%.

The roundness test raises an interesting question: if all 16 diameters are the same does that guarantee that your "ball" is perfectly round? The answer is clearly no: at most, 16 equal diameters might determine the location of 32 points around a centre; then we can easily fill in the spaces between those points with flat polygons, and the resulting polyhedron will be perfect according to FIFA's test.

So, what if FIFA decides to be super careful and to test the infinitely many possible diameters, in all directions? Does this finally guarantee that the soccer ball is perfectly round? No!

You may recall that we wrote about shapes of constant diameter that are not circles. An example is the rounded blue "triangle" illustrated below. Now, spin this triangle on its bottom point, like a top. The result is a solid shape of constant diameter: it will be judged perfect by even the super-careful FIFA test.

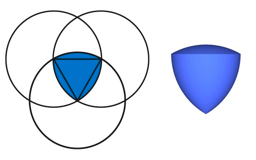
Does this mean that FIFA is using a silly test? No, not really. But there are indeed more reliable methods of testing roundness than simply to measure a couple of diameters. And in situations that are more life-and-death than a soccer game, diameter tests should be avoided.

One such case, where the life-and-death was all too real, was the Columbia space shuttle disaster. The inquiry following the disaster uncovered a number of serious shortcomings in the running of the shuttle program. One shortcoming, although not one responsible for the disaster, was a test for roundness of rocket parts: NASA's test consisted of nothing more than measuring and comparing three diameters.

Puzzle to Ponder: Feel free to suggest solutions in the comments section. Please also email us if you wish to be added to our email list.

Suppose you have a mystery object and that its shadow (with the Sun directly above) is a perfect circle. You rotate the object and still the shadow is a perfect circle, and you rotate once more with the same result. Do the three circular shadows guarantee that your mystery object is a perfect sphere?

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator. 

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

http://www.qedcat.com/

Copyright 2004-∞ All rights reserved.