We have it pegged

Burkard Polster and Marty Ross

The Age, 6 October 2014

The other day a very excited little maths mistress returned home from school carrying a "brand new game". A quick inspection revealed it to be the age-old game of Peg Solitaire. Still, it turns out that there are interesting new things to say about this very old game.

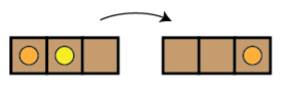
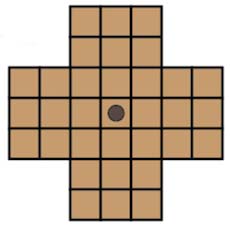
For those unfamiliar with Peg Solitaire here is a quick reminder of the rules. The game begins with every space except for the centre occupied by a marble (or peg), as pictured above. A move in the game consists of one marble jumping horizontally or vertically over another marble into an adjacent space, and then removing the jumped marble.

The goal of the game is to finish with just one marble, in the middle of the board.

Before reading further the reader may wish to try the game here or here for a few minutes. Or hours, or days.

Peg Solitaire is not easy. Typically we'll be caught with two or more marbles and no possible moves. And, even if we succeed in removing all but one marble, chances are this last marble will not be located in the centre. We won't tell you how to win the game; that'd spoil the fun, and anyone who really feels the need to cheat can easily find recipes on the internet.

Instead we'd like to point out and explain a surprising observation: if the game ends with just one marble remaining then that marble must be in one of the five spaces pictured below.

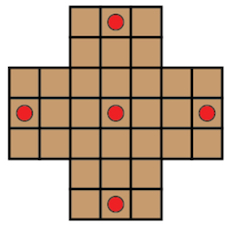
Why would that be so, and how could we possibly hope to prove it except by playing through every possible game? With the right approach it all turns out to be quite easy and very pretty.

To investigate the game we'll employ the gadget pictured below. It consists of two light bulbs, labelled Left and Right, each controlled by an on-off button.

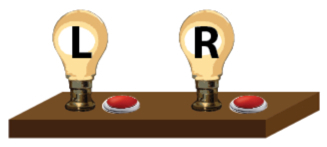
We also label the solitaire board as follows:

Now, whenever a marble is either removed from or placed on an L-space, we push the L button. Similarly, the R-spaces are our triggers to hit the R button, and the LR-spaces instruct us to hit both buttons. So, what can happen?

Let's begin with the solitaire board entirely empty and with both lights off. Now we add marbles one by one, switching the lights on and off as we go, until we're at the starting arrangement for Solitaire. Will the lights then be on or off?

There are ten LR-spaces (not counting the centre), eleven L-spaces and eleven R-spaces. So, no matter the order in which the marbles are placed, both buttons will be pushed 21 times, and that means both lights will be on when all the marbles are in position.

Now let's play a game of Solitaire. There are only four possible beginning moves, one of which is indicated by the yellow circle above. The only place to move the marble in the circled R-space is to the centre LR-space, and we then remove the marble on the L-space between them.

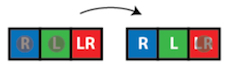
In effect two marbles are removed and one marble is added. Accordingly, we will hit both the R button and the L button twice, and both lights will still be on after our move.

And that demonstrates the trick, the key observation: after any move at any stage of the game, both lights will stay on. It is easy to see that any move will involve marbles being placed or removed from three spaces, one of each type, resulting in both Left and Right lights being switched off and then on again.

So, however the game ends it must do so with both lights on. But then supposing there is only one marble left, where could it be? Removing the last marble will leave an empty board, at which stage we know that both lights must be off. It follows that this last marble must have been on one of the LR-spaces:

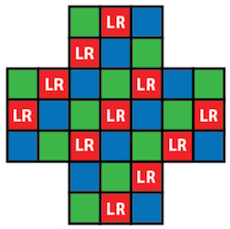
That's limited the possible endings and we can now easily limit them further. If we had started with the mirror-image labelling, the exact same argument would have proved that the final marble must be in one of the "mirror" LR-spaces:

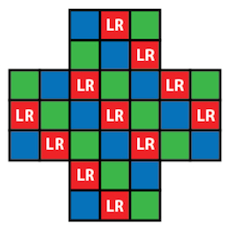
It follows that the final marble must actually be in one of the overlap LR-spaces, so one of the five spaces we indicated above. That completes the very pretty proof.

This same clever idea can be used to analyse many variations of Solitaire, with some nice surprises. Suppose, for example, your local Solitaire Master is becoming a little smug. Then you can present him with the 7 x 7 Solitaire game pictured below. You can make it even easier for him, allowing the final marble to wind up wherever he wishes.

It turns out this new game is impossible and it is now easy for us to prove that this is so. As above, we set up our light gizmo and label the board:

There will be 16 spaces of each type (not counting the centre), which means that if the empty board had both lights off then so will the board at the start of our game. But then with just one marble remaining both lights must still be off, and that's impossible: removing the last marble would result in an empty board with at least one light on.

This is all very cute, but is there any deeper meaning? Not surprisingly, yes.

Our lightbulb gizmo is a simple example of what is known as a mathematical invariant: a quantity that remains unchanged when certain transformations are performed. There is much more that invariants can say about Peg Solitaire, and the keen reader might wish to continue here or here.

Mathematical invariants play very important roles in many branches of mathematics. At times they provide beautifully simple answers to what appear to be fiendishly difficult questions. Alas, at other times the invariants simply fail to help; for example there are Solitaire configurations that our gizmo will fail to rule out but which are in fact impossible to solve.

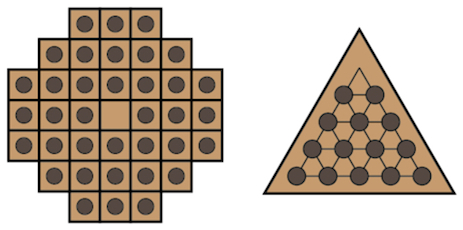
But that's enough deeper meaning for one column: it's time to get back to work. (No, not your boss's work. Of course that can wait.) Pictured below are two more Solitaire boards, the second of which can played online here. What does our invariant gizmo say about them? Can the games actually be solved? We'll expect your completed homework in the comments section below.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.