The Maths Masters' Summer Quiz

Burkard Polster and Marty Ross

The Age, 9 December 2013

Here it is: our sixth annual Summer Quiz. We offer you 30 puzzles, some easy and some definitely not so. This year, we've sourced many of the puzzles from the excellent collections The Number Detective, Math Charmers, Je mehr Löcher, desto weniger Käse and Mindbenders and Brainteasers.

Answers to all of the puzzles will appear on our website on December 13, and we will post detailed solutions on December 16.

This is our final column for 2013, and your Maths Masters will begin a long (possibly well-earned) break. Happy holidays to all our readers, and we look forward to bringing you more Maths Masterish fun in the New Year. Happy puzzling!

EASY

Easy 1

Five couples go to a party and everybody shakes hands with everybody else. How many handshakes are there? What if each person shakes hands with everyone excepting their partner?

Easy 2

A cylindrical drinking glass is three times as tall as it is wide. Which is greater, the height of the glass or its circumference?

Easy 3

Find all pairs of prime numbers that add up to 999.

Easy 4

In the Mix & Match book pictured above every page consists of a top, a middle and a bottom. It is promised that there are "over 300 mix-ups". What is the smallest number of pages the book could have?

Easy 5

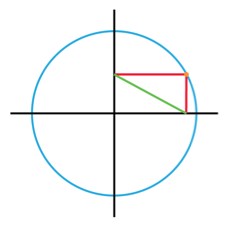
If the diameter of the circle above is 2, how long is the green segment?

Easy 6

Norbert tosses a coin four times. What are the chances that the coin comes up tails every time? What are the chances of Norbert getting tails on exactly three of the four tosses?

Easy 7

There are 50 teachers At Maths Masters High School. Yesterday 152 letters were delivered for the teachers, and Ms. Noether received more letters than anybody else. What is the smallest number of letters that Ms. Noether could have received?

Easy 8

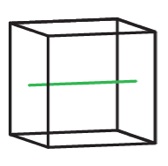
An axis of a cube is a line about which we can rotate the cube and after which the cube is back in its original position. For example, the cube above can be rotated 90, 180 or 270 degrees around the green line. (360 degree rotations don't count!) How many axes does a cube have?

Easy 9

In a recent council election, Bernard received the most votes: 73 more than Henri, 87 more than Karl, and 95 more than Augustin. There were 1233 votes in total. How many votes did Bernard receive?

Easy 10

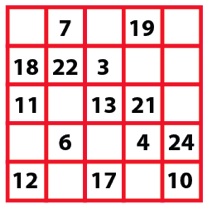
Complete the magic square above. All the numbers from 1 to 25 must be used, and every row, column and diagonal must sum to the same number.

MEDIUM

Medium 1

Isaac takes a 2-digit number, adds 1 to it and divides by 2. The result is Isaac's number but with the digits reversed. What was Isaac's original number?

Medium 2

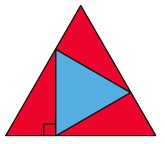
An equilateral triangle is inscribed inside a larger equilateral triangle, as pictured above. If the big triangle has area 1, what is the area of the smaller equilateral triangle?

Medium 3

Sonya grabs an equal number of marbles in each hand. She transfers 4 of the marbles from her left hand to her right. She counts the remaining marbles in her left hand, throws them away and throws away the same number of marbles from her right hand. Finally, she picks up 5 marbles in her left hand. How many marbles does she have in the end?

Medium 4

Niels and Évariste each earn $2000 per month. At the beginning of February Niels receives a pay rise of 10%, and at the beginning of April he receives a pay cut of 10%. Who will earn more money over the year?

Medium 5

In the picture above does the green rectangle cover more or less than half of the red rectangle?

Medium 6

Carnival Conway offers you a game, where you throw three (normal) dice. If one 6 comes up then you win $20, for two 6s you win $50, and if all three dice come up 6 you win $100; otherwise, you lose $20. Is this a fair game? How much, on average, would you win or lose?

Medium 7

Hermann wants to hike across a desert. The trip will take 6 days but a single person can only carry sufficient water for 4 days. How many helpers will Hermann require to cross the desert? Assume that any helpers are also meant to survive.

Medium 8

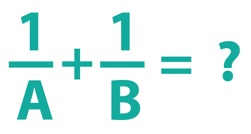
The sum of two numbers is 2 and the product of the same two numbers is 3. What is the sum of the reciprocals of the two numbers?

Medium 9

Poker Polya deals out cards from a deck one by one. How many cards must Polya deal out until he is sure that a flush (five cards of the same suit) has appeared amongst the dealt cards? What if Polya wants a straight (five cards in sequence, with an ace counting low or high)?

Medium 10

Something went wrong in a chocolate factory. There are three piles of chocolate bars. Two of the piles consist of bars correctly weighing 100 grams, however all the bars in the third pile weigh 95 grams. Using a digital scale and just one weighing, how do you determine which pile has the dodgy chocolate bars?

HARD

Hard 1

Split the numbers above into three groups of three numbers each, so that the product of the numbers in each group is equal.

Hard 2

Lucky Leonhard is playing a casino game. He places his bet and then rolls a pair of dice: if the dice sum to 7, 8 or 9 then Leonhard wins the amount of his bet, and otherwise Leonhard loses his money. Leonhard begins with $100 and decides to bet $50 at time, until he has either won $100 or has gone broke. What are the chances that Leonhard leaves the casino a winner?

Hard 3

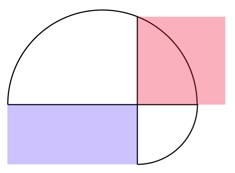
In the above picture the top curve is a semicircle and the bottom curve is a quarter circle. Which has greater area, the red square or the blue rectangle?

Hard 4

Felix wants to move the pictured log into the position indicated by the dotted line. The log is so heavy that Felix can only lift up one end and rotate the log around the other end. How many such moves does Felix require to accomplish his task.

Hard 5

In a 100 meter race, Jacob can beat Johann by 5 meters, and Johann can beat Nicolaus by 10 meters. By how much can Jacob beat Nicolaus?

Hard 6

The above are two pretty equations: six consecutive numbers with the sum of the first three giving a two-digit number and the sum of the second three resulting in the same number but with the digits reversed. Are there any other such examples?

Hard 7

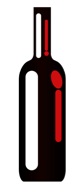
René has a 16 ounce bottle of wine. On the first day he drinks 1 ounce and then fills the bottle back up with water. On the second day he drinks 2 ounces of the mixture in the bottle and then again fills the bottle with water. The next day he drinks 3 ounces, and so on, until on the 16th day he drinks the full contents of the bottle. How much water did René drink?

Hard 8

What is the above sum?

Hard 9

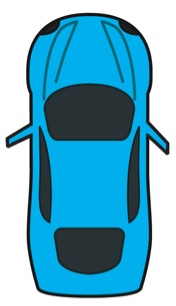
Is the steering wheel on the left or right side of the car?

Hard 10

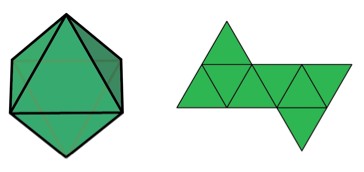
Above is pictured an octahedron ("diamond") together with one if its nets: a way of cutting open the octahedron along its edges so that it is still all connected but can lie flat on the table. The octahedron has 11 nets in total: can you find them all? (Reflected and rotated nets are not considered to be different.)

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is helping Barbie smash calculators and iPads with a hammer.