Parabolic production line

by Burkard Polster and Marty Ross

The Age, 17 June 2013

One of your Maths Masters is blessed to have a very young Maths Mistress to assist him with his work. Regular readers of this column will not be surprised that little Eva's favourite word is “cat”. She loves cats. Amusingly, though, it seems that everything is a cat. Eva greets all animals (including her parents) with a loud and confident cry of “Cat!”

Eva's omni-catting is oddly familiar. It is reminiscent of many high school maths classes, where any curvy graph is as likely as not to be greeted with confident cries of “parabola!”

The parabola-spotting is significantly less amusing, but of course it is not the students' fault. The textbooks overflow with parabolas and quadratic equations, including the most absurdly contrived applications: what to make of a shop displaying x²+ 2x - 48 types of cheese? Moreover, students are introduced to few other curves, which are seldom distinguished in a meaningful or memorable manner.

It is all sad and silly. And needless. There are genuine, beautiful applications of parabolas which are rarely if ever discussed. Yes, eventually a few lucky students briefly study projectile motion (and seemingly more briefly when the senior Australian Curriculum kicks in), but that's about it.

Physics students still see such applications, in the form of parabolic mirrors and lenses. These are welcome mainstays of science museums such as Scienceworks, particularly as very impressive parabolic whispering walls.

Wouldn't it be refreshing for students to know how these displays work, beyond parroting “focal point” as if reciting jargon explains anything? Wouldn't it be worthwhile for students to know what a focal point is, and the mathematics to explain it? We live in (not overly much) hope.

One day we'll give focal points a go. Today, however, we'll demonstrate a simpler and very cool feature of parabolas.

Last year, one of your Maths Masters visited the Mathematikum in Giessen, Germany. This is a seriously amazing mathematics museum, featuring many impressive exhibits (including a parabolic whispering wall). One exhibit was based upon a parabola drawn on a white wall:

What appear as black dots on the parabola are cylinders protruding from the wall. The numbers on the coordinate axes indicate that the parabola is the archetypal y = x², with the cylinders placed at points with whole number coordinates.

The purpose of the exhibit is to demonstrate how to graphically multiply two numbers. To find 3 x 4, for example, the visitor is instructed to tie a rope between the cylinders at distances 3 and 4 to the left and right of the vertical axis. This is represented by the straight red line in the following diagram.

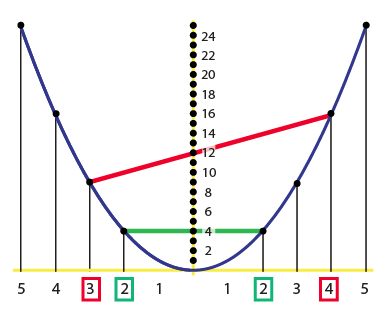
Then, the spot where the rope crosses the vertical (y) axis indicates the product of the two numbers. So, in the above example we have demonstrated that 3 x 4 = 12. Very nice!

It is a surprising and clever demonstration, but why does it work? It's not hard to understand when the two numbers are the same (so we're simply squaring a single number): in this case the rope will be horizontal and at just the correct height. This is illustrated in the previous diagram, the green line indicating the product 2 x 2 = 4.

If the numbers A and B to be multiplied are unequal there is more work to be done. A natural approach is to begin by obtaining the equation of the straight red line. However, it is simpler to just draw in horizontal and vertical lines, creating a big red triangle:

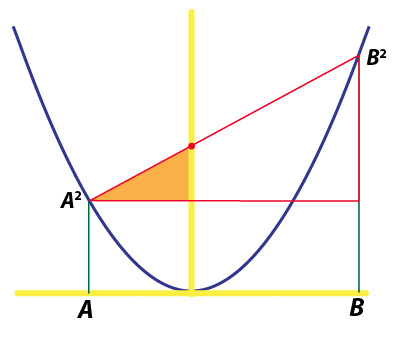
Then, we notice that the smaller triangle inside is similar (that is, it's the same shape). It is then straightforward to use this similarity to obtain an equation, indicating where the red line crosses the vertical axis. (We'll leave the details to the triangle aficionados.)

What about negative numbers? The Mathematikum exhibit only demonstrated the multiplication of positive numbers, but the same construction works just as well in general. Below, for example, we have calculated 2 x (– 5) = –10.

This graphical multiplying is very pretty, and it also has a very pretty consequence: it can locate for us all the prime numbers. Or, rather, it can locate all the numbers that are not prime.

Consider all possible multiplications of two whole numbers greater than one, and draw the straight lines for each of these multiplications. Then, every possible product will be indicated by a line running through the vertical axis. The only numbers left untouched will be 1 and the prime numbers. It is a striking, pictorial variation of the famous sieve of Eratosthenes.

It's all very nice stuff and we could write plenty more, but that's probably enough parabolic fun for one day. After all, there's serious schoolwork to get done: somewhere out there is a cheese shop that desperately needs factorizing.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.