Fibonacci, Steve Jobs and the Devlin in the details

Many readers of this column would be familiar with the Fibonacci sequence. It begins 1, 1, 2, 3, 5, 8, 13, with each number the sum of the two preceding numbers. (So, the next number in the sequence would be 8 + 13 = 21, and then 13 + 21 = 34 and so on.) But who was Fibonacci and what did he really do? It turns out that there is a little less and very much more to the mathematician than his megafamous numbers.

Leonardo Pisano, better known as Fibonacci, was born around 1170, probably in Pisa (as his name suggests). He produced a number of mathematical works, the first and most famous being Liber Abbaci. It is this book, which first appeared in 1202, that contains Fibonacci's eponymous sequence.

Liber Abbaci is huge, the English translation running to 600 pages. Obviously there is much more to it than one peculiar sequence of numbers. Indeed, Liber Abbaci was truly revolutionary.

The Latin title translates as “Book of Calculation”, which sums up the book perfectly. Liber Abbaci was a massive textbook on arithmetic and algebra, complete with hundreds of worked examples.

That doesn't sound particularly interesting, let alone revolutionary, but Liber Abbaci was essentially the first mathematics textbook of modern Europe. Algebra was invented and applied centuries earlier, by Arabic mathematicians: the word is derived from the Arabic al-jabr, meaning “restoration”. However, algebra was practically unknown in Europe prior to Fibonacci.

Fibonacci's algebra didn't look much like our modern version since there was no X or the like to stand for the unknown quantity; it was another 350 years before algebra became symbolic. And, if symbolic algebra famously causes students headaches, non-symbolic algebra is migraine material.

Consider, for example, the following problem from Chapter 11 of Liber Abbaci:

A certain man buys 30 birds which are partridges, pigeons and sparrows, for 30 denari. A partridge he buys for 3 denari, a pigeon for 2 denari, and 2 sparrows for 1 denaro, namely 1 sparrow for 1/2 denaro. It is sought how many birds he buys of each kind.

Hmmm. The answer is hardly evident. Nonetheless, a modern student can get going by letting P stand for the number of partridges, and similarly G and S stand for the numbers of pigeons and sparrows. Then, since 30 birds were bought in total, we know that

P + G + S = 30

And, since the birds cost 30 denari in total, it follows that

3P + 2G + S/2 = 30

And again, hmmm. However, at least the above equations have neatly extracted the information provided: we've escaped the words. (We'll leave the reader to further escape the equations.) By contrast, Fibonacci's solution is all words.

Fibonacci's text is not an easy read, even (especially?) for a modern reader. Fortunately, we have available an excellent guide.

Keith Devlin is an English mathematician residing in America. He is a very well known (and accomplished) populariser of mathematics: similar to your Maths Masters but much more prominent. In 2011, Devlin released The Man of Numbers, a superb biography of Fibonacci.

Devlin's book, subtitled Fibonacci's Arithmetic Revolution, focusses upon the contents and the influence of Liber Abbaci. As the subtitle suggests, it was Fibonacci's arithmetic even more than his algebra that was truly revolutionary.

How could that be? Algebra may have been new to Europeans, but of course they had been multiplying and dividing numbers for centuries. What was there to revolutionise?

As well as algebra, Fibonacci imported another brilliant mathematical invention: the Hindu-Arabic numerals. These are the familiar 1, 2, 3 and so forth, including the all-important 0. They are the building blocks of our now standard base ten notation.

Prior to Fibonacci, Europeans calculated almost exclusively with Roman numerals: I, V, X and so on. This made arithmetic, and so essentially all of mathematics, incredibly cumbersome. Apart from the pain of coping with the everyday mathematics of finance and commerce, Roman numerals made any genuine mathematical advance impossible. That all changed after the appearance of Liber Abbaci (give or take a century or two of stubborn resistance).

So, Fibonacci truly started a mathematical revolution, giving birth to modern mathematics in Europe. However, there is a puzzle.

Fibonacci was not the first European to write on Arabic mathematics. Indeed, though it seems likely that Fibonacci could read Arabic, it is also certain that when writing Liber Abbaci he referred to existent translations of Arabic texts. Moreover, Hindu-Arabic numerals first appeared in Europe 250 years earlier (though the 0 took a while longer), in essentially the same form that we see them now:

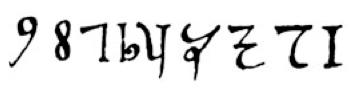
So, why should Fibonacci get all the credit? That's where Devlin brings in Steve Jobs, the genius behind Apple computers, as a point of comparison.

Keith Devlin visited Melbourne last summer and one of your Maths Masters had the pleasure of meeting him. He also had the pleasure of attending Devlin's brilliant lecture, Leo and Steve. (Devlin also gave a lecture on mathematical modelling, with a regrettably amoral discussion of drones, but we'll let that rest.)

In his book and his lecture (a version of which can be viewed here), Devlin explained why Fibonacci's work had such an impact. Fibonacci was a superb mathematician, but Liber Abbaci, mathematically meticulous though it was, was not written for the few scholars of the time. Rather, Fibonacci wrote a textbook, a manual for the thousands who had a practical use for the mathematics. Fibonacci sold the new (for Europe) mathematics to the merchants and tradesmen.

That's where Devlin makes the insightful comparison of Fibonacci to Steve Jobs. Devlin distinguished the invention with the packaging and promotion of that invention.

Jobs no more invented the personal computer than Fibonacci introduced Arabic mathematics to Europe. What Jobs (and others) did was package the personal computer in a manner which made it accessible and made its power apparent, so that millions could see the computer as important, or even essential.

Devlin's lecture went deeper, with some fascinating historical detective work to emphasise his point. Though Fibonacci's influence had never seriously been doubted, the means of that influence was unclear. The puzzle was that the many simpler arithmetic texts that followed Fibonacci seemed to strongly resemble each other but to not be directly based upon Liber Abbaci. There was a missing link.

The mystery was only solved very recently, by Italian historian Rafaella Franci. It turns out that the missing link was Fibonacci himself.

It was known that Fibonacci had written another book, Libro di Minor Guisa, "Book in a Smaller Manner", but no original had survived. However, in 2003 Franci found an anonymous manuscript from the late 13 century. This manuscript, written in the vernacular rather than Latin, was essentially a Cliff's Notes version of Liber Abbaci. It was also clearly the basis of the later arithmetic texts. Moreover, there is very strong evidence that the manuscript was a transcription (and perhaps translation) of Fibonacci's Guisa.

So, Fibonacci inspired the European mathematical revolution with Liber Abbaci. He then furthered his own revolution in the most practical way possible, with a no-nonsense manual.

And what of the Fibonacci sequence in all this? It was nothing more than a simple example in Liber Abbaci, a bit of light relief between the more serious problems. Moreover, as Devlin notes, the "Fibonacci numbers" had been discovered and rediscovered a number of times, beginning at least 1500 years before Fibonacci.

So, the one piece of mathematics for which Fibonacci is universally known is not even his, and is microscopic in comparison to his genuine contribution. Such is the fickleness of mathematical fame.

Puzzle to Ponder: Can you solve Fibonacci's bird problem?

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.