Demystifying the Möbius

The Möbius strip is one of mathematics' superstars. It is an endless source of puzzlement and beauty, and all you need to make one is a thin strip of paper. Give the strip a 180 degree twist, staple together the ends and you have your Möbius strip.

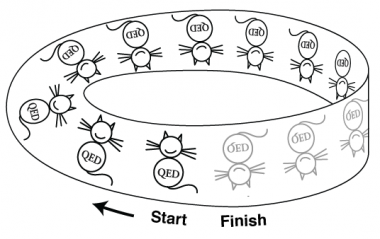
Most famously the Möbius strip is one-sided: a flat QED cat travelling along one side of the strip will end up on the other side. However, there are many other wonders to be had. Last year we demonstrated a lovely Valentine's Day trick, creating interlocked hearts from two joined Möbius strips.

But where's the maths? Yes, it's all well and good to demonstrate some curiosities of twisted paper strips. Indeed it's great to do that: many mathophobes have been won over by such demonstrations. However an explanation or two also wouldn't go astray. We'll now attempt to make amends.

The above photograph features four paper loops with differing numbers of twists. On top are the cylinder (no twists) and the Möbius strip (one twist). At bottom left, the strip casting the impressive infinity shadow has two twists. Finally, at the bottom right is a triple-twisted loop, recognizable as the omnipresent recycling logo.

Of course we can create twistier loops, and we can imagine loops with any number of twists. However, experimenting with the loops above suffices to give a very clear idea of what happens in general.

The different loops behave differently but they naturally fall into two groups, depending upon whether the number of twists is even or odd. We'll begin by considering the simpler, albeit less thrilling, even-twisted loops.

The plain old cylinder can be considered the simplest of the “even”-twisted loops, but there's not much to say about it. It has two sides, and a top edge and a bottom edge, and that's about it.

The genuinely even-twisted loops are more interesting. They each have two sides, just like the cylinder. However, cutting along the waist of such a loop results in two new, interlocking loops. Not bad! 

The odd-twisted loops, including the familiar Möbius strip, are a lot more interesting. To begin, they are all one-sided. (For this and related reasons, mathematicians would normally refer to all of the odd-twisted loops as Möbius strips. However, we'll ignore this technicality and reserve the “Möbius” label for the traditional, single-twist loop.)

The fun really begins if you cut an odd-twisted loop along its waist. When this is performed on a Möbius strip the result is not two loops, but rather one long loop. This is one of the first and one of the best tricks in any Möbius strip presentation.

The waist-cutting trick is even more impressive when performed on one of the other odd-twisted loops. The result is again one long loop but in this case the loop has tied itself in a knot. Very cool indeed.

Now, how to explain all this? It turns out to be quite easy.

To make any of our loops we begin with a paper strip with two long edges. We've highlighted them in red and green below. 

The edges of the strip then become the edge(s) of the loop, and this is where the importance of having an odd or even number of twists becomes clear. If there is an even number of twists then the two ends of the green edge will join, resulting in a green circular edge. Smilarly, the loop will have a completely red edge, and so two edges in total, just as for the cylinder.

However, if the loop has an odd number of twists then the red and green edges will be connected into one long multicoloured circle. Moreover, cutting along the waist will not separate any of the paper loop from this single circular edge; that demonstrates that the waist-cutting cannot split an odd-twisted loop into two loops.

It is just as easy to see that the even-twisted and odd-twisted loops have two and one sides respectively. Colour the two sides of the original strip red and green, make your twists and see how the colours line up where the ends of the strip are joined.

Finally, there is a clever way to see how those knots arise. Below we've highlighted the single edge of the triple-twisted loop.

Now, imagine cutting the loop along its waist with a special, thick pair of scissors, so all the white part of the paper disappears. All that is left, then, is the red edge, which clearly forms a knot. 

Performing the real cutting with a regular pair of scissors, the resulting loop will follow exactly the same path as the red knot. So, the newly created loop will form a knot as well. This approach also easily shows why waist-cutting the doubly-twisted loop results in the two linked loops.

So there you have it: a number of the most popular Möbius tricks explained. But is any of this serious mathematics? Does it really matter? Yes it is, and yes it does.

In topology, the mathematics that is concerned with the fundamental shape of things, the Möbius strip becomes much more than a source of clever parlour tricks. It turns out to be as central to the study of surfaces as the notions of odd and even are for the understanding of whole numbers.

But today is playtime, and you can return to the fun and surprises of paper loops. We'll keep the more serious maths lesson, and some more Möbius surprises, for another day.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.