Six of one, Babylonian the other

The Wonders of Mesopotamia is an excellent exhibition now on display at Melbourne Museum. The exhibition features fascinating Sumerian and Babylonian artifacts, many over 4000 years old. And, what is really excellent is that the very first artifact you meet is a mathematical gem.

"Babylon" has a special resonance for mathematicians. Referring both to the ancient Mesopotamian civilisation of Sumer and (more accurately) to the empires that followed, Babylon is generally considered to be the birthplace of mathematics. Moreover, later Babylonian mathematics was in many ways astonishingly advanced.

Of course, deciding when and where mathematics was born depends upon what we mean by "mathematics". Tally sticks have existed for at least 30,000 years, and it seems clear that counting in some form or another is much older. So, we might just declare the first mathematician to have been Og the Caveman (not his real name).

However, numbers only take on their full mathematical role when we begin doing things with them. So it's perhaps more realistic to date mathematics to the beginning of measurement and arithmetic. And it seems that all that took off between 3000BC and 3500BC, coinciding with the emergence of cities and large scale agriculture.

Of course for any such society to function, some arithmetic and geometry is essential: there are fields to measure, seasons to predict, products to weigh and to sell, and so on. So, if the Sumerians were the original mathematicians it was perhaps necessarily so; theirs was simply the first civilisation of sufficient size and complexity. However, this is where the questions begin.

A civilisation may well putter along with just enough mathematics to make do. That seems to have been true of the contemporaneous Egyptian kingdoms. It was most definitely true of the later Roman Empire, which actually lost the wealth of Greek mathematics gifted to them. But, it was decidedly not true of the Babylonians.

By about 1600BC, Babylonian mathematicians had made some stunning achievements: they knew about "Pythagoras's" Theorem (a good thousand years before Pythagoras was born); they could solve essentially all quadratic equations, and many similar equations; they had excellent methods for approximating square roots; they had many formulas for areas and volumes of geometric figures. And, generally, it appears that the Babylonians developed a very strong sense of algebraic methods; their thinking was inventive and abstract.

True, there were also some relative clangers. Some of the Babylonian geometric formulas were badly inaccurate, and it seems that they never did better than 3 1/8 as an approximation for π. Nonetheless, all in all, Babylonian mathematics was genuinely brilliant, in some ways outclassing the much heralded Greek mathematics that followed.

So, how? How did Babylonian mathematics progress so far? No one knows for sure, but it seems likely that one peculiar aspect, dating back to early Sumerian times, had an enormous effect: Babylonians were really keen on the number 6.

That just raises bigger questions. What's so thrilling about 6? And how could a preference for one number lead to such general accomplishments?

More precisesly, the key is the number 60, which is of course 6 x 10, and it all started with the early Sumerians' choice of 60 as a principle unit of measurement. The earliest Sumerian writing, around 3000BC, contained the following numerals (all easily produced by poking a stylus into the clay tablets they used for writing):

Then, general numbers were indicated by repeating the appropriate numerals, just as is done with Roman numerals. For example, one of the earliest recorded numbers is

Given our own deci-centric society this choice of 60 may at first seem very strange, but it was actually extremely natural and functional. Because 60 has so many factors, the Sumerians were able to handle many division problems with ease: fractions of one unit of measure were often whole amounts of another. It's exactly why we still divide an hour into 60 minutes, a circle into 360 degrees and so on.

It is not clear that the Sumerian use of 60 encouraged the next step, but a general ease of calculation couldn't have hurt. And it was a huge step: at some point, around 2000BC, a very intelligent Babylonian had the revolutionary idea to introduce positional notation.

This is the same system we use today, where numerals do double duty, or more. In the number 747, for example, the first 7 stands for seven hundreds, and the second 7 stands simply for seven. In this way, we can easily and economically write any whole number using only the ten numerals 0, 1, 2, ..., 9.

The Babylonians used positional notation in exactly the same manner. So, they had a ones place, a 60s place, a 60 x 60 = 3600s place, and so on. However, given the Babylonian method of repeating numerals, they got by with just two symbols:

(The Babylonians had no symbol for 0 and no concept of 0 as a number, which created ambiguities in Babylonian positional notation. These ambiguities were clarified by spacing and context. Later, a placeholder symbol was introduced, which effectively played the role of 0.)

Now, for example, our huge Sumerian number above would be written in Babylonian positional notation as

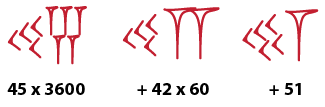
For the Babylonians to come up with positional notation was hugely impressive, and it was not to be rediscovered for over two thousand years. However, the Babylonians went further, and their next step was almost certainly facilitated by the use of 60 as a base.

We use positional notation to represent not only very big numbers but also very small ones: that is, we have the decimal representation of fractions. For example, we can write 1/4 as 0.25, with 2 in the tenths place and 5 in the hundredths place. The Babylonians took the analogous step: they introduced a 1/60 place, a 1/3600 place and so on.

Moreover, due to 60's many factors, Babylonian sexagesimal representations were typically much simpler than our decimals. For example, since 1/4 = 15/60 this fraction could be written by the Babylonians with just 15 in the 1/60 place. An even more telling example is 1/3, which didn't bother the Babylonians at all, while we have to resort to an infinite decimal.

The above table of reciprocals illustrates the benefits of 60 as a base, and also that 60 was not a cure-all. The reciprocal 1/7 could only be expressed as an infinite repeating sexagesimal, just as we would write it as an infinite repeating decimal. Indeed, Babylonian tables of reciprocals often left out such problematic examples, though they did have methods for obtaining approximations to these fractions.

But the underlying truth remains, that the Babylonian numerical system made many arithmetic computations easy. That freed Babylonian minds to explore deeper ideas, and it made it cleaner and easier to explore those ideas. The result was the creation of some very beautiful mathematics.

And that very first artifact in the Museum's exhibition? It is a clay tablet, one of these Babylonian tables of reciprocals: as we said, a mathematical gem.

Puzzle to Ponder: Melbourne Museum has produced classroom materials to accompany the Babylonian exhibition, with some excellent exercises on Babylonian numerals. For a harder puzzle, what is the infinite Babylonian sexagesimal for 1/7? 

Free Public Lecture, August 12: Marty will give a presentation, The Mathematical Gardens of Babylon, at the Melbourne Museum, 10:30-11:30. For more information and to register, please visit the MAV website.

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.