We get a Lotto calls

A fortnight ago there was a big jackpot ready to go off in Tuesday’s Oz Lotto.  As is standard when these jackpots appear, mathematicians received a succession of calls from the media.

We would have thought that a simple “Buckley’s chance” aptly sums up the likelihood of any given person winning. However, it seems that the public loves to hear official mathematical versions from official mathematicians. So, as we have in the past, your maths masters obliged. 

First, let’s get the Buckley part out of the way and figure out the chances of our lottery ticket winning the jackpot.

On our Oz Lotto ticket we mark off seven numbers from 1 to 45. Then, 45 numbered balls are placed into a machine and seven balls are drawn out. Our ticket will win the jackpot (Divison 1) if we have correctly chosen the seven drawn numbers.

To figure out the chances of doing this, we can calculate ball by ball. For the first ball there are 45 numbers that might come up and 7 of those would match a number on our ticket. That means we have a 7/45 chance of our ticket still being in the running after the first ball is drawn.

Suppose we have correctly chosen the first ball. There are then 44 balls left and we have 6 numbers left on our ticket to match them. So, at that stage we have a 6/44 chance of our ticket surviving the second ball.

Working through all seven balls, we can see that the chances of choosing all seven numbers correctly, and so being able to retire to a tropical island, is

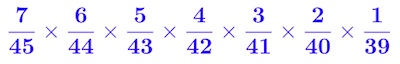
That works out to about 1 chance in 45 million. (Actually, 1 chance in 45,379,620, for those who want to know the precise value of a Buckley.)

This is small in comparison to the numbers we have considered in our recent columns (here and here), but it’s still plenty large. How can we get a sense of it?

Newspaper reports of lottery jackpots always include comparisons to unlikely events, such as being hit by lightning. Here is one stunning comparison that was suggested to us by a colleague.

Below is a diagram of the MCG, and at left full forward you can see a black dot. Now, imagine dropping a dart from high above the MCG and assume it hits somewhere randomly on the field. What are the chances of the dart hitting that black dot? It’s clearly not very likely, and the chances of winning Oz Lotto are much less. 

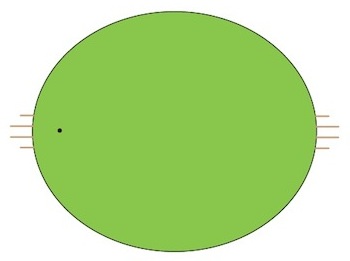
The dot we have drawn represents a circle of about 2 meters in diameter. However, the chances of winning Oz Lotto correspond to hitting a circle that is 2 centimeters in diameter, about the size of a 10 cent coin. To put it another way, your chances of winning the jackpot in Oz Lotto are about 1/10,000 the chance of hitting the “large” dot we’ve actually drawn.

(The black dot that would actually represent winning Oz Lotto is too small for the screen resolution. However, we have made a similar hi-res pdf, which you can download from our website. If you have the pdf printed on A0 paper, the dot should (just) appear).

OK, so after all that, it is clear that our chances of winning Oz Lotto are about what we originally suspected: Buckley’s. However, there’s another interesting question we can ask.

As it happens, there was no Division 1 winner in Oz Lotto two weeks ago. Was that surprising? What were the chances that someone would win?

It seems that the actual number of lottery tickets was around 50 million, but let’s cheat a bit and assume that there were 45 million tickets; that is, we assume there were just enough tickets to cover every combination. Of course, many combinations would have been repeated and so many other combinations would not have been covered at all.

Now we consider each ticket in turn. The chances of the first ticket not winning were (45 million – 1)/(45 million). And, the same was true for all 45 million tickets. To find the chances that none of the tickets would win we multiply the individual chances, and that gives

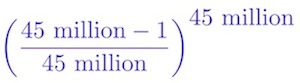
We can easily throw that into a calculator, but there is a very interesting alternative. Rearranging the fraction slightly, we can rewrite the expression as

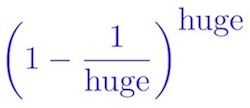
where “huge” happens to equal 45 million. And now, this may ring a bell.

Last year, we considered the quantity (1 +1/huge)^huge. The end result (as “huge” gets into the zillions) is defined to be the famous (not Euler’s) number e, which is about 2.7.

It takes some fiddling, which we’ll leave for you as a puzzle, but it turns out that our new expression, (1 –1/huge)^huge, is very close to the reciprocal 1/e, which is about 0.37. That’s the chance that no one would win the jackpot, leaving about a 63% chance of a winner.

So, with that many tickets entered, we’d expect that there’d be a winner, but it’s not a huge shock that there wasn’t. And of course, with everyone and their dog buying tickets the following week, it was no surprise at all that the jackpot went off last Tuesday.

Puzzles to ponder: Supposing that 90 million tickets are entered into tomorrow night’s Oz Lotto, what are the chances that someone will win? The main step in the 1/e calculation is to show that  1/(1 – 1/huge) = 1+ 1/(huge - 1): can you do that?

Burkard Polster teaches mathematics at Monash and is the university's resident mathemagician, mathematical juggler, origami expert, bubble-master, shoelace charmer, and Count von Count impersonator.

Marty Ross is a mathematical nomad. His hobby is smashing calculators with a hammer.

www.qedcat.com

Copyright 2004-∞ All rights reserved.